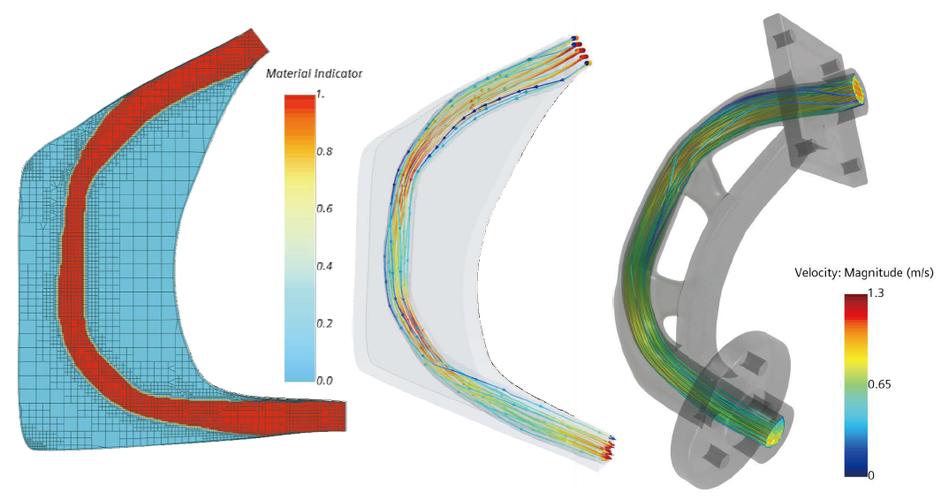
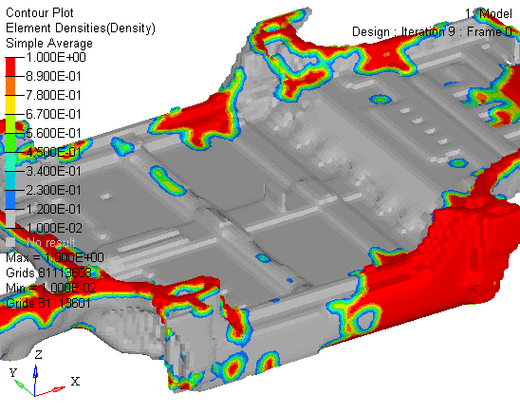
显式拓扑优化方法研究是结构设计领域的重要研究方向,旨在通过数学规划算法直接优化材料的分布,以实现结构性能与轻量化目标的平衡,与传统的隐式方法相比,显式方法通过显式定义材料插值模型和目标函数,能够更高效地处理复杂约束条件,并在工程实践中展现出较高的计算精度和稳定性。
在显式拓扑优化方法中,材料插值模型是核心环节之一,常见的插值模型包括SIMP(Solid Isotropic Material with Penalization)模型和RAMP(Rational Approximation of Material Properties)模型,SIMP模型通过引入惩罚因子,将中间密度材料的弹性模量进行非线性衰减,从而有效促进材料向0-1分布收敛,其数学表达式为E(ρ)=E_min+ρ^p(E_0-E_min),为密度变量,p为惩罚因子(通常取3),E_0和E_min分别为实体材料和空洞材料的弹性模量,而RAMP模型则采用有理近似函数,通过调整参数控制材料属性的平滑过渡,其在处理复合材料优化问题时具有更好的适应性,下表对比了两种模型的优缺点:
| 模型类型 | 优点 | 缺点 |
|---|---|---|
| SIMP模型 | 计算简单,收敛性好,适用于大规模问题 | 对惩罚因子敏感,易产生棋盘格现象 |
| RAMP模型 | 材料属性过渡平滑,优化结果更易加工 | 计算复杂度较高,参数标定难度大 |
显式拓扑优化的数学模型通常以结构柔顺度最小化为目标函数,同时满足体积约束和平衡方程,其标准形式为:min C(ρ)=F^T U,s.t. V(ρ)/V_0≤f_max,K U=F,0≤ρ≤1,其中C为柔顺度,F为载荷向量,U为位移向量,K为刚度矩阵,V为结构体积,V_0为设计域体积,f_max为体积约束上限,为求解该非线性规划问题,常用的算法包括优化准则法(OC)、移动渐近线法(MMA)以及序列二次规划法(SQP),OC算法通过推导最优性条件,采用显式更新规则调整材料密度,具有计算效率高的优势;MMA算法则通过构造一系列近似显式子问题,能够处理复杂的非线性约束,适用于多目标优化问题。
近年来,显式拓扑优化方法在多个领域得到广泛应用,在航空航天领域,通过优化飞机机翼或卫星支架的拓扑结构,可实现减重30%-50%的同时满足强度和刚度要求,在汽车工业中,该方法被用于设计轻量化底盘和车身结构件,有效提升了燃油经济性和碰撞安全性,生物医学工程领域则利用拓扑优化设计个性化植入物,如人工关节和骨替代材料,通过仿生结构设计提高生物相容性和力学匹配度,显式方法仍面临一些挑战,如多物理场耦合问题的计算效率、大规模问题的内存消耗以及优化结果的可制造性处理等,为解决这些问题,研究者们正致力于发展并行计算算法、拓扑优化与增材制造的集成设计方法,以及基于机器学习的代理模型技术,以进一步提升显式拓扑优化方法的工程实用价值。
相关问答FAQs:
-
问:显式拓扑优化方法与隐式方法的主要区别是什么?
答:显式方法通过显式定义材料插值模型和目标函数,直接求解材料分布问题,计算过程透明且易于控制;而隐式方法通常通过水平集或相场等间接描述材料界面,需要求解偏微分方程,计算复杂度较高,显式方法在处理大规模工程问题时具有更高的计算效率,但可能面临局部最优解的问题;隐式方法在描述复杂拓扑边界时更具优势,但计算成本较大。 -
问:如何提高显式拓扑优化结果的可制造性?
答:可从三个方面入手:一是引入尺寸约束和最小特征尺寸控制,避免生成过薄的悬臂结构;二是在优化后处理中采用几何平滑算法,如滤波技术或形态学操作,消除棋盘格效应和锯齿边界;三是结合增材制造工艺特点,设计支撑结构或梯度密度过渡区域,确保优化结果能够通过3D打印等先进制造技术准确实现,部分研究者还开发了基于制造规则的拓扑优化算法,直接在优化过程中考虑工艺约束,进一步提升设计方案的可行性。