资本市场研究中的资本资产定价模型(CAPM)是现代金融理论的基石之一,由威廉·夏普(William Sharpe)在1964年提出,与约翰·林特纳(John Lintner)和简·莫森(Jan Mossin) independently 发展,共同奠定了该模型的基础,CAPM旨在描述在均衡条件下,资产的风险与其预期收益率之间的关系,为投资者提供了一种量化风险溢价、评估资产定价合理性的工具,同时也成为资产配置、投资组合管理和公司资本预算决策的重要理论依据。
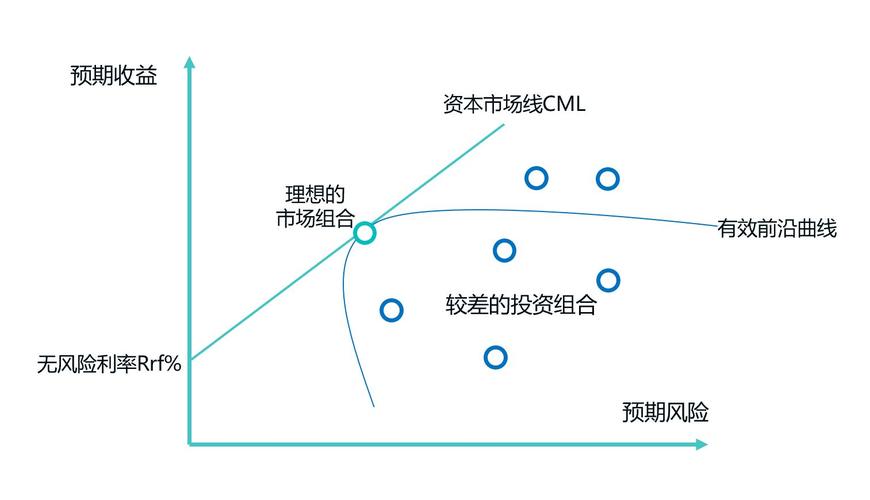
CAPM的核心思想在于,投资者承担风险时要求获得相应的回报,而资产的总风险可分为系统性风险(不可分散风险)和非系统性风险(可分散风险),非系统性风险可通过多元化投资消除,因此不应获得额外收益;系统性风险则源于宏观经济、市场整体等因素,无法通过分散化消除,投资者需要承担此类风险并获得补偿,CAPM通过β系数(Beta)来衡量资产相对于市场的系统性风险水平,构建了以下基本公式:
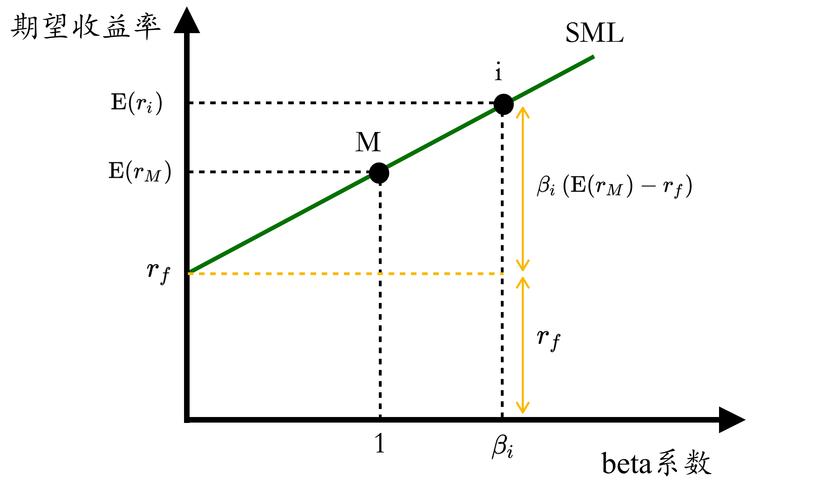
[ E(R_i) = R_f + \beta_i (E(R_m) - R_f) ]
( E(R_i) ) 表示资产 ( i ) 的预期收益率;( R_f ) 为无风险收益率(通常以短期国债利率为代表);( E(R_m) ) 为市场组合的预期收益率;( \beta_i ) 为资产 ( i ) 的β系数,反映资产收益率对市场收益率变动的敏感性;( (E(R_m) - R_f) ) 为市场风险溢价(Market Risk Premium),是投资者因承担市场系统性风险要求的超额回报。
β系数的计算基于资产收益率与市场收益率的历史数据回归分析,其公式为:
[ \beta_i = \frac{\text{Cov}(R_i, R_m)}{\text{Var}(R_m)} ]
( \text{Cov}(R_i, R_m) ) 为资产 ( i ) 收益率与市场收益率的协方差;( \text{Var}(R_m) ) 为市场收益率的方差。β值的经济含义如下:若β=1,表示资产的系统性风险与市场平均水平相当,预期收益率等于市场收益率加无风险利率;若β>1,资产风险高于市场(如科技股),预期收益率更高;若β<1,资产风险低于市场(如公用事业股),预期收益率较低。
CAPM的假设条件较为严格,包括:投资者是风险厌恶型的,且仅关注预期收益率和标准差;投资者可以无限制地以无风险利率借贷;市场信息完全对称,无交易成本和税收;所有投资者持有相同的市场组合(以所有风险资产按市值加权构成),这些假设使CAPM在现实应用中存在局限性,例如现实中存在交易成本、税收和信息不对称,且投资者的风险偏好并非完全一致。
尽管存在争议,CAPM在资本市场研究中仍具有重要应用价值,在资产定价方面,CAPM为评估股票、债券等资产的合理价格提供了基准,若某股票的实际预期收益率高于CAPM计算结果,则可能被低估(存在买入机会);反之则可能被高估,在投资组合管理中,投资者可根据自身风险偏好,通过调整不同β系数资产的配置比例,构建符合收益风险目标的组合,风险承受能力强的投资者可增加高β资产比例以追求更高收益;保守型投资者则可配置低β资产,CAPM在公司金融领域用于计算资本成本(Cost of Equity),作为项目评估的折现率,企业使用CAPM估算股权资本成本后,结合债务成本计算加权平均资本成本(WACC),以判断新投资项目是否创造价值。
CAPM的实证检验也引发了广泛讨论,早期研究(如Fama & French, 1992)发现,公司规模(Size)和账面市值比(Book-to-Market)对收益率具有解释力,β系数的显著性较弱,对“CAPM失效”的质疑推动了多因子模型(如Fama-French三因子模型)的发展,后续研究指出,早期实证设计存在数据偏差,且在考虑不同市场周期和资产类别后,β系数仍具有一定的解释力,在市场暴跌期间,高β资产往往跌幅更大,符合CAPM对系统性风险的刻画。
以下是CAPM中关键变量的定义与解释:
| 变量符号 | 名称 | 经济含义 | 计算方式/代表指标 |
|---|---|---|---|
| ( E(R_i) ) | 资产预期收益率 | 投资持有资产 ( i ) 的期望回报 | 基于历史数据或分析师预测估算 |
| ( R_f ) | 无风险收益率 | 无风险投资(如国债)的回报率 | 通常采用短期国债(如3个月期T-bill)利率 |
| ( E(R_m) ) | 市场预期收益率 | 整个市场组合(如沪深300、标普500)的期望回报 | 市场指数历史平均收益率或预测值 |
| ( \beta_i ) | 贝塔系数 | 资产 ( i ) 相对于市场的系统性风险 | 资产收益率与市场收益率的回归斜率 |
| ( (E(R_m) - R_f) ) | 市场风险溢价 | 市场组合超过无风险收益率的溢价 | 历史市场平均收益率减无风险利率(如6%-8%) |
CAPM的局限性也不容忽视,其假设的“市场组合”在现实中难以精确界定(通常用股票指数代替,未包含房地产、商品等资产);无风险利率在通胀环境下可能不稳定;β系数基于历史数据,未来风险特征可能发生变化,行为金融学指出,投资者并非完全理性,情绪偏差可能导致资产短期偏离CAPM预测。
尽管如此,CAPM因其简洁性和直观性,仍是资本市场研究的核心框架之一,后续的多因子模型(如Fama-French三因子、Carhart四因子)可视为对CAPM的扩展,而非完全替代,CAPM揭示了“风险与收益正相关”的基本原理,为理解资产定价逻辑提供了基础,投资者需结合市场环境和资产特性,灵活运用该模型进行决策。
相关问答FAQs
Q1: CAPM中的β系数如何影响投资决策?
A1: β系数是衡量资产系统性风险的关键指标,直接影响投资者的预期收益要求,若某资产的β>1,表明其波动性高于市场,适合风险承受能力强的投资者,以换取更高的风险溢价;若β<1,则风险较低,适合保守型投资者,在牛市中,高β资产可能获得超额收益;但在熊市中,其跌幅也可能更大,投资者可通过β系数调整资产配置:当预期市场上涨时,增加高β资产比例;当市场不确定性增加时,降低β以控制风险,基金经理可通过β系数构建“市场中性”组合(如做多低β资产、做空高β资产),对冲系统性风险。
Q2: CAPM在现实中存在哪些局限性,如何改进?
A2: CAPM的主要局限性包括:假设条件过于理想化(如无交易成本、完全信息),市场组合难以精确定义,β系数的稳定性不足,以及未考虑规模、价值等风险因子,改进方法包括:使用多因子模型(如Fama-French三因子模型)补充β解释力,引入行为金融学理论修正投资者理性假设,或采用前β(Pre-beta)等动态指标捕捉风险变化,可结合行业特征调整β系数(如科技行业β普遍高于公用事业行业),或使用条件CAPM(Conditional CAPM)考虑宏观经济状态对风险溢价的影响,以提高模型在现实中的适用性。