“数学广角”是人教版小学数学教材中一个非常独特且重要的板块,它并非传统意义上的知识点章节,而是一个旨在渗透数学思想方法、培养学生数学思维和解决问题能力的专题单元。

下面,我将从多个维度对“数学广角”进行深入剖析。
什么是“数学广角”?
核心定义: “数学广角”是人教版小学数学教材中的一个特色模块,它不以传授新的数学知识(如计算、公式)为主要目的,而是通过生动有趣、贴近生活的情境和活动,有计划、有步骤地向学生渗透一些重要的数学思想方法。
核心理念: 从“知识传授”转向“能力培养”,让学生在“做中学”、“玩中学”,感受数学的魅力,学会用数学的眼光观察世界,用数学的思维分析问题。
定位: 它是连接“具体生活问题”与“抽象数学思想”之间的桥梁,是培养学生核心素养(如逻辑推理、模型意识、应用意识)的重要载体。
“数学广角”研究什么?(主要内容与思想方法)
“数学广角”的内容编排遵循小学生的认知规律,由浅入深,螺旋上升,其主要研究并渗透的数学思想方法包括:
排列与组合
- 核心思想: 分类讨论,有序思考。
- 探究在一定的条件下,事物如何进行搭配、排列或组合,以及有多少种不同的可能性。
- 典型问题:
- 搭配问题: 有2件上衣和3条裤子,一共有多少种不同的穿法?(乘法原理的雏形)
- 排列问题: 用数字1、2、3可以组成多少个不同的两位数?(注意顺序,如12和21是不同的)
- 组合问题: 从3个同学中选2个去参加比赛,一共有多少种选法?(不注重顺序,如选A和B与选B和A是同一种)
- 教学目标: 让学生初步感受到“有序”思考的重要性,学习用列表、画图等方法解决问题,避免重复和遗漏。
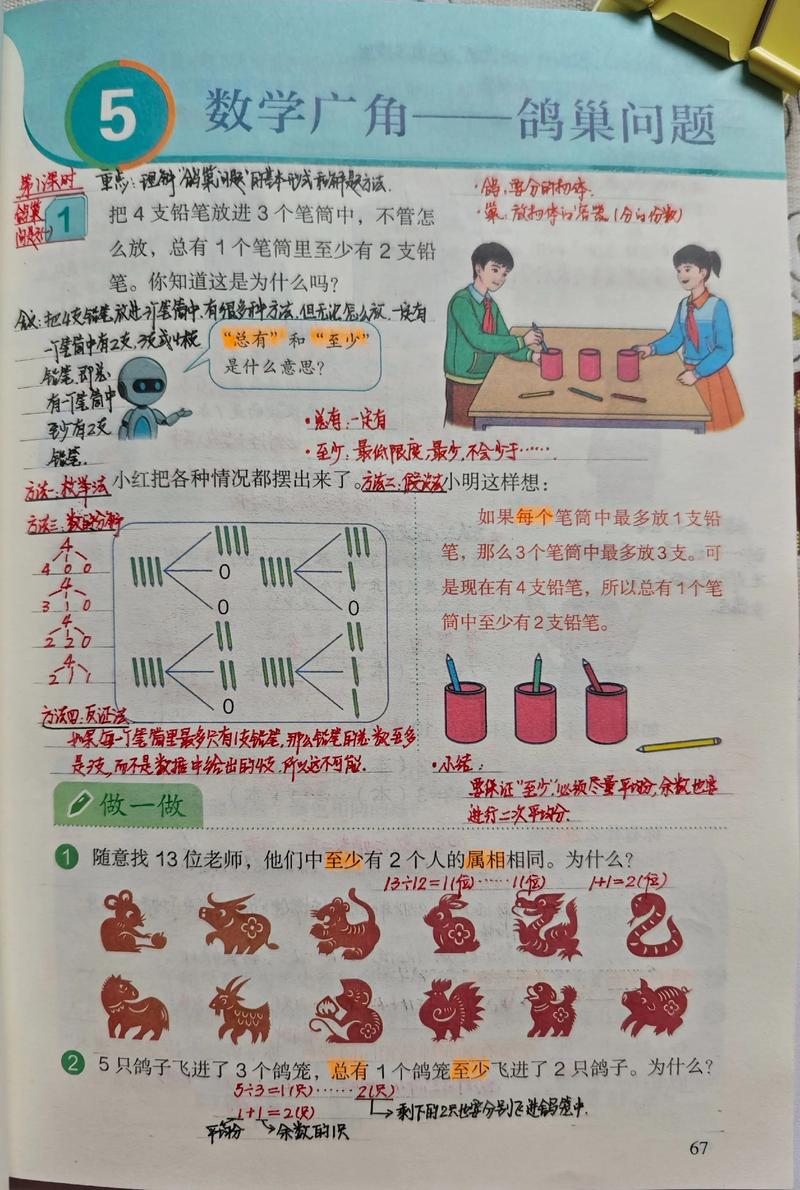
鸡兔同笼问题
- 核心思想: 假设法、方程思想(用算术方法体现)、逻辑推理。
- 这是一个经典的算术问题,旨在培养学生分析问题、运用多种策略解决问题的能力。
- 典型问题: 笼子里有若干只鸡和兔,从上面数,有35个头;从下面数,有94只脚,问鸡和兔各有多少只?
- 教学目标:
- 假设法: 假设全是鸡,那么脚的总数会少多少?少的脚数是因为把兔子当成了鸡,每只兔子少算了2只脚,从而求出兔子的数量。
- 列表法: 通过列表尝试,从“全是鸡”或“全是兔”开始,逐步调整,找到正确答案。
- 目标: 体验解决问题策略的多样性,感受数学的逻辑性和趣味性,为后续学习方程思想打下基础。
植树问题
- 核心思想: 模型思想,数形结合。
- 探究在一条线段上植树,间隔数、棵数与总长之间的关系。
- 典型问题:
- 两端都栽: 棵数 = 间隔数 + 1
- 只栽一端: 棵数 = 间隔数
- 两端都不栽: 棵数 = 间隔数 - 1
- 教学目标: 引导学生通过画线段图等方式,将实际问题抽象成数学模型,理解“间隔”这一核心概念,并学会根据不同的情况灵活解决问题。
找次品/优化问题
- 核心思想: 优化思想,策略最优化。
- 如何用最少的次数,从一堆物品中找出一个不合格的(如较轻或较重的)次品。
- 典型问题: 有3瓶钙片,其中1瓶是次品(轻一些),用没有砝码的天平至少称几次能保证找到次品?如果是9瓶呢?
- 教学目标: 让学生体验解决问题策略的优劣,理解“三分法”是最优策略,培养其追求效率和优化的意识。
等量代换
- 核心思想: 等量关系,代换思想。
- 用一个未知量去代替与它相等的另一个未知量,从而简化问题。
- 典型问题: 1个苹果 = 2个梨,1个梨 = 4个草莓,那么1个苹果等于几个草莓?
- 教学目标: 初步建立等量观念,理解“相等”可以互相替换,为学习代数中的“代入”思想做准备。
烙饼问题/沏茶问题
- 核心思想: 统筹优化,合理安排。
- 如何在完成多项任务时,合理安排顺序,使总用时最短。
- 典型问题: 一个平底锅每次可以烙2张饼,每面需要3分钟,烙3张饼至少需要几分钟?
- 教学目标: 培养学生的优化意识和时间管理能力,学会从整体上考虑问题,寻找最优方案。
“数学广角”的教学策略与挑战
教学策略:
- 情境化教学: 创设生动有趣、贴近学生生活的情境(如穿衣搭配、猜球游戏、侦探破案),激发学生的学习兴趣。
- 活动化探究: 鼓励学生动手操作、小组合作、自主探究,通过摆一摆、画一画、写一写、说一说等方式,亲身体验解决问题的过程。
- 可视化思维: 大量运用画图、列表、连线等直观手段,将抽象的数学思想“可视化”,帮助学生理解和内化。
- 策略多样化: 鼓励学生从不同角度思考,用不同方法解决问题,并引导他们比较不同策略的优劣,体验优化思想。
- 语言表达: 引导学生用清晰、有条理的语言描述自己的思考过程,培养其逻辑表达能力。
面临的挑战:
- 思想抽象,难以量化: 数学思想方法本身是抽象的,不像知识点那样有明确的“对错”标准,评价学生的掌握程度比较困难。
- 教师专业素养要求高: 教师自身必须深刻理解所渗透的数学思想,才能有效地引导学生,避免将课上成简单的“解题技巧课”。
- 课时有限,深度不足: 由于课时安排较少,教学容易停留在表面活动,难以深入挖掘其背后的数学思想。
- 与应试的平衡: 在应试压力下,部分教师可能认为“广角”内容不直接考,从而忽视或弱化其教学。
“数学广角”的价值与意义
- 提升核心素养: 它是培养学生逻辑推理、数学建模、直观想象、数据分析等数学核心素养的最佳载体。
- 激发学习兴趣: 趣味性和挑战性并存,能有效改变数学“枯燥乏味”的刻板印象,让学生爱上数学。
- 培养高阶思维: 它超越了单纯的计算和记忆,专注于培养学生的分析、综合、评价、创造等高阶思维能力。
- 衔接中学数学: 所渗透的假设、代换、模型、优化等思想,是中学代数、几何、概率统计学习的重要基础。
- 落实“双减”精神: “数学广角”强调思维过程而非题海战术,符合“减负增效”的教育改革方向。
总结与展望
“数学广角”是人教版小学数学教材的一大创举,它标志着小学数学教育从“知识本位”向“素养本位”的重要转变,它不仅仅是一些有趣的问题,更是一个承载着数学灵魂、旨在塑造学生思维方式的平台。
未来研究展望:
- 跨版本教材比较研究: 对比其他版本教材(如苏教版、北师大版)中类似板块的设计理念与内容,取长补短。
- 教学评价体系研究: 如何科学、有效地评价学生对数学思想方法的掌握程度,是一个亟待研究的课题。
- 信息技术融合研究: 如何利用动画、交互式软件等技术,更生动地展示抽象的数学思想过程。
- 与STEM教育的结合: 将“数学广角”中的问题与科学、技术、工程项目相结合,提升学生的综合应用能力。
深入研究并上好“数学广角”,对于培养适应未来社会发展需要的、具有强大思维能力的新一代,具有不可估量的深远意义。