数学教育研究课题类型丰富多样,涵盖理论探索、实践应用、技术开发等多个维度,旨在推动数学教育的改革与发展,这些课题类型既关注数学教育的本质规律,也注重解决实际教学中的问题,同时结合时代发展需求引入新兴技术与理念,以下从不同角度对主要课题类型进行详细阐述。
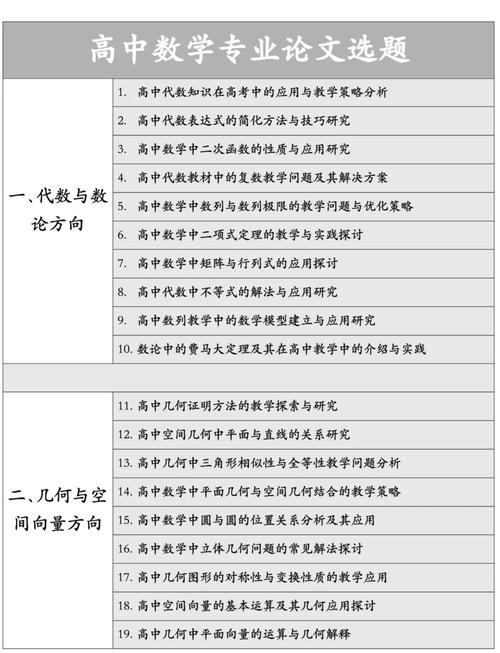
理论建构与政策研究类课题
此类课题侧重于数学教育的基础理论、政策框架及历史发展研究,旨在为教育实践提供理论支撑和政策指导,数学教育哲学研究探讨数学的本质、数学知识的认知方式及其教育价值,分析不同哲学观(如绝对主义、可误主义)对教学目标的影响;课程政策研究则聚焦国家或地区数学课程标准的制定逻辑、实施效果及修订方向,如核心素养导向下的课程内容重构研究,数学教育史研究通过梳理国内外数学教育演变历程,揭示社会文化、科技发展对数学教育观念的塑造作用,为当前改革提供历史借鉴。
课程与教材研究类课题
课程与教材是数学教育的核心载体,此类课题围绕内容设计、结构优化及实施效果展开,具体包括:数学课程的国际比较研究,分析不同国家课程标准的差异(如美国的共同核心州立标准与中国的义务教育数学课程标准),提炼可借鉴的经验;教材内容的适切性研究,探讨如何将抽象数学概念与学生生活经验、认知水平结合,统计与概率”领域教材中情境设计的真实性研究;跨学科整合课程研究,如数学与科学、工程、艺术等学科的融合路径,探讨STEAM教育理念下数学课程的创新模式,教材使用效果研究通过课堂观察、师生访谈等方法,评估教材在实际教学中的应用情况,为教材修订提供依据。
教学与学习研究类课题
此类课题是数学教育研究的核心,聚焦教学实践、学习过程及师生互动,按研究重点可分为三类:一是教学方法研究,如探究式教学、项目式学习、翻转课堂等模式在数学课堂中的应用效果,比较不同方法对学生问题解决能力、高阶思维发展的影响;二是学习规律研究,通过认知心理学视角分析学生的数学概念形成过程、错误类型及成因,分数概念”的阶段性认知发展研究,或数学学习困难学生的认知特征与干预策略;三是师生互动研究,探讨课堂提问、反馈方式、小组合作等互动要素对学生参与度和学习动机的影响,如教师等待时间对学生数学表达质量的作用研究。
技术融合与创新研究类课题
随着信息技术的发展,技术赋能数学教育成为重要研究方向,此类课题包括:教育工具开发与应用,如动态几何软件(GeoGebra)、数学建模平台、自适应学习系统的设计与实践,分析技术工具对学生空间想象能力、抽象思维能力的促进作用;在线教育模式研究,探讨疫情期间线上数学教学的成效与问题,构建“线上+线下”混合式教学的有效路径;人工智能在数学教育中的应用,如基于学习分析的学生个性化学习路径推荐系统,或AI辅助的数学作业自动批改与错误诊断技术,技术伦理与公平性问题也受到关注,如数字资源分配不均对学生数学学习机会的影响研究。
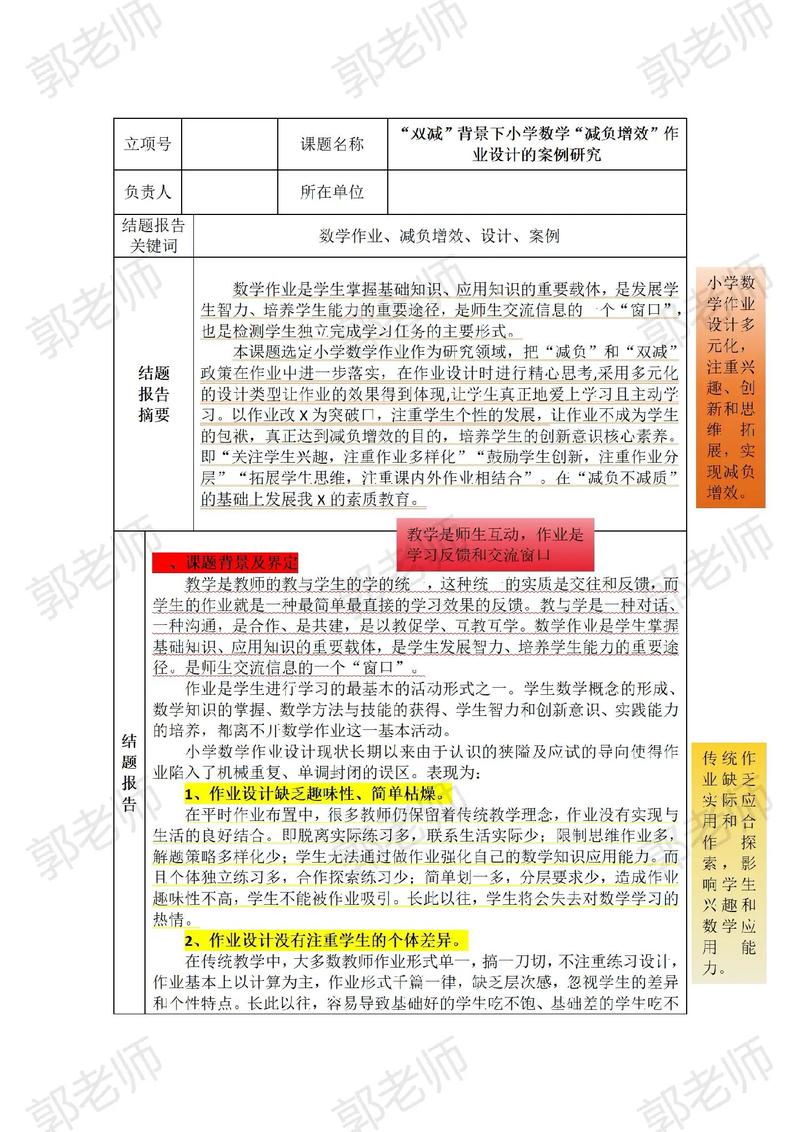
评价与 assessment 研究类课题
数学评价是教育质量的关键保障,此类课题聚焦评价理念、方法及工具的创新,过程性评价研究探讨如何通过课堂观察、学习档案袋、表现性任务等方式全面评估学生的数学核心素养,突破传统纸笔测试的局限;评价标准研究,如基于核心素养的数学学业质量标准制定,或国际大型评估项目(如PISA、TIMSS)的数学素养框架本土化应用;评价结果的应用研究,分析如何将评价数据转化为教学改进的依据,例如通过学生错题分析调整教学策略,评价公平性研究关注不同性别、地域、家庭背景学生的数学成绩差异及其背后的社会文化因素。
教师专业发展研究类课题
教师是数学教育改革的实施者,此类课题关注教师的知识结构、能力提升及职业发展,具体包括:教师知识研究,如数学学科内容知识(PCK)的构成与发展,分析专家教师与新教师在教学设计、学生认知把握上的差异;教师培训模式研究,探索“课例研究”“行动研究”“校本研修”等培训方式的实效性,或基于社区的教师学习共同体构建;教师信念研究,探讨教师对数学本质、学生学习的看法如何影响其教学决策,数学是否可教”的信念对学生错误处理方式的影响;教师职业倦怠与激励研究,分析数学教师工作压力来源及职业幸福感提升策略。
特殊群体与公平教育研究课题
此类课题关注数学教育中的公平性问题,聚焦弱势群体的学习需求,农村地区数学教育质量提升研究,分析资源匮乏背景下如何通过教师培训、课程优化缩小城乡差距;性别与数学学习研究,探讨社会文化因素对女生数学兴趣和成就的影响,促进性别公平;特殊需求学生的数学教育研究,如自闭症学生的数学教学策略,或学习障碍学生的数学认知干预;多元文化背景下的数学教育研究,如少数民族地区数学课程中的文化融入,或移民学生的数学语言适应问题。
跨学科与前沿交叉研究课题
数学教育与其他学科的交叉融合催生新兴研究方向,数学与神经科学的交叉研究,通过脑成像技术(如fMRI)探索学生数学思维的神经机制;数学教育社会学研究,分析家庭背景、学校文化、社区资源对学生数学参与度的影响;数学教育经济学研究,探讨数学教育与个体职业发展、区域经济增长的关联,未来教育趋势研究,如人工智能时代数学核心素养的重新定位,或元宇宙技术在数学沉浸式学习中的应用前景,也属于此类课题。
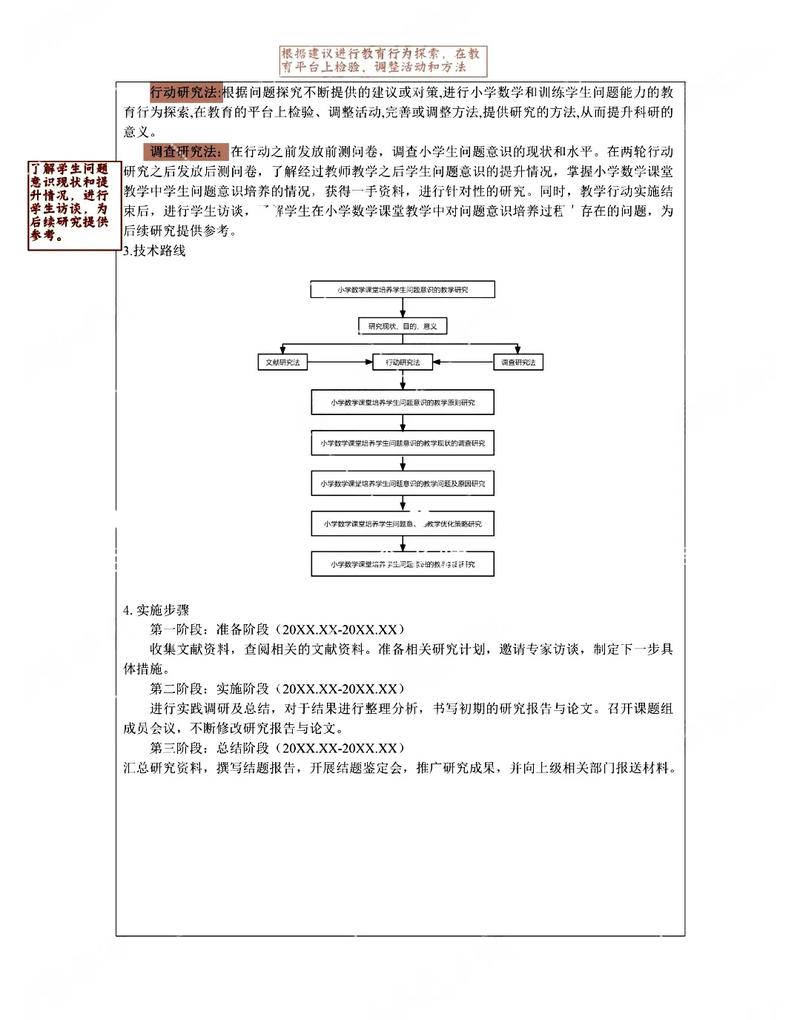
以下表格总结了主要课题类型及其研究重点:
| 课题类型 | 研究重点 |
|---|---|
| 理论建构与政策研究 | 数学教育哲学、课程政策、历史发展 |
| 课程与教材研究 | 设计、教材适切性、跨学科整合 |
| 教学与学习研究 | 教学方法、学习规律、师生互动 |
| 技术融合与创新研究 | 教育工具开发、在线教育模式、人工智能应用 |
| 评价与 assessment 研究 | 过程性评价、评价标准、结果应用 |
| 教师专业发展研究 | 教师知识、培训模式、职业信念 |
| 特殊群体与公平教育研究 | 弱势群体需求、性别差异、文化融入 |
| 跨学科与前沿交叉研究 | 神经科学机制、社会文化影响、未来教育趋势 |
相关问答FAQs
Q1:如何选择适合的数学教育研究课题?
A:选择课题需结合个人兴趣、研究资源与实践需求,通过文献综述梳理领域内热点与空白,避免重复研究;考虑研究的可行性,如数据获取难度、研究方法的适用性;关注教育实践中的真问题,如何提升学生的数学建模能力”比“数学建模理论研究”更具实践价值,建议与导师或同行讨论,明确研究范围与深度,确保课题兼具理论意义与应用价值。
Q2:数学教育研究中的混合方法设计是什么?如何应用?
A:混合方法研究结合定量(如问卷调查、实验设计)与定性(如访谈、课堂观察)方法,通过数据三角验证提升研究效度,在“探究式教学对学生数学焦虑的影响”研究中,可采用定量方法(焦虑量表前后测)分析数据变化,同时通过定性方法(学生访谈、课堂记录)探究焦虑变化的深层原因,应用时需明确两种方法的逻辑关系(如解释性序列设计:定量结果→定性解释),并注意方法间的整合,避免数据割裂。